Salam. Halo sahabat Ahzaa, selamat datang kembali di AhzaaNet. Pada kesempatan
ini saya membagikan Latihan Soal Tes Akademik Matematika Penerimaan Tamtama Polri Tahun
Anggaran 2023.
Beberapa waktu yang lalu Kepolisian Negara Republik Indonesia membuka
penerimaan Tamtama POLRI untuk gelombang I tahun 2023. Berdasarkan
informasi dalam pendaftaran tersebut, teman- teman bisa memilih
Tamtama Brimob atau Tamtama Polair. Setiap peserta yang
mendaftar, akan melalui beberapa tahapan seleksi, dimulai dari seleksi
administrasi, kesehatan, psikologi, akademik, kesamaptaan dan lain-
lainnya. Salah satu tes yang diujikan dalam seleksi penerimaan Tamtama
POLRI adalah tes akademik. Tes akademik tersebut mencakup materi
(1) Pengetahuan umum (PU) (termasuk UU Kepolisian);
(2) Wawasan kebangsaan (WK) (Pancasila, UUD 1945, NKRI, Bhinneka Tunggal Ika,
wawasan nusantara dan Kewarganegaraan);
(3) Bahasa Inggris (B.ING);
(4) Matematika (MTK)
Nah, untuk mempersiapkannya, berikut saya sajikan latihan salah satu dari soal
akademik di atas khususnya untuk mapel MATEMATIKA (MAT). Materi untuk latihan
soal tes akademik Matematika adalah Matematika Dasar. Latihan soal sudah saya
lengkapi dengan pembahasan setiap soal untuk memudahkan dalam belajar.
Baca Juga :
|
|
Photo by Randy Tarampi on Unsplash |
Semoga saja latihan ini dapat memberikan referensi baru bagi teman-
teman yang sedang belajar giat menghadapi ujian seleksi masuk Tamtama
Kepolisian.
Nah, langsung saja, berikut latihan soal- soalnya, Selamat Berlatih. Semoga
sukses semuanya dan jangan lupa bagikan pada teman- teman lain seperjuangan.
======================================================================================
Latihan Soal Tes Akademik Matematika Penerimaan Tamtama POLRI Tahun 2023 Plus
Pembahasan
1. Pak Adi bekerja selama 6 hari dengan 4 hari diantaranya lembur mendapat
upah Rp. 74.000, 00. Pak Budi bekerja selama 5 hari dengan 2 hari di antaranya
lembur dan mendapat upah Rp. 55.000,00. Pak Adi, Pak Budi dan Pak Dudi bekerja
mendapatkan upah yang sama. Apabila Pak Dudi bekerja selama 5 hari dengan
terus menerus lembur, maka upah yang akan diperoleh adalah ....
A. Rp. 60.000,00
B. Rp. 63.000,00
C. Rp. 70.000,00
D. Rp. 74.000,00
E. Rp. 76.000,00
6x + 4y = 74.000 ............................... i)
5x + 2y = 55.000 ............................... ii)
Kedua persamaan di atas diselesaikan dengan cara eliminasi
6x + 4y = 74.000 X 1 ----> 6x + 4y = 74.000
5x + 2y = 55.000 X 2 ----> 10x + 4y = 110.000
_______________________________________
-4x = -36.000
x = 9000
6x + 4y = 74.000
----> y = (74.000-6x)/ 4
y = (74000- 6. 9000)/4
y = (74.000 - 54.000)/4
y = 5000
Jadi, upah yang diterima Pak Dudi adalah
(5 x Rp.9000) + (5 x Rp. 5000)
45.000 + 25.000
= Rp. 70.000,00
2. Nilai rata- rata ulangan IPA dari 30 siswa adalah 7. Kemudian 5 orang siswa
mengikuti ulangan susulan sehingga nilai rata- rata keseluruhan menjadi 6,8.
Nilai rata- rata siswa yang mengikuti ulangan susulan adalah ....
A. 6,8
B. 5,6
C. 5,3
D. 4,9
E. 4,8
n2 = 5
35 . 6,8 = 30 . 7 + 5 . x2
x2 = (238 - 210)/ 5
= 5,6
3. Jangkauan kuartil dari susunan bilangan 3, 4, 7, 8, 5, 9 adalah ....
A. 4
B. 4,5
C. 5
D. 6,5
E. 6
Apabila bilangan- bilangan 3, 4, 7, 8, 5, 9 tersebut diurutkan, maka menjadi
Jangkauan interquartil adalah Q3 - Q1
= 8 - 4
= 4
4. Dari sehelai karton akan dibuat sebuah kotak tanpa tutup dengan alas
bujur sangkar. Jika jumlah luas bidang alas dan semua bidang sisi kotak
ditentukan sebesar 432 cm2, maka volume kotak terbesar yang mungkin
adalah ....
A. 723 cm3
B. 782 cm3
C. 816 cm3
D. 864 cm3
E. 912 cm3
Luas permukaan = 432 cm2
panjang = lebar = x dan tinggi = t, maka
x2 + 4xt = 432 ===>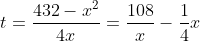 
Volume kubus :
v = x2 . t = (108/x) - (1/4)x
= 108x - (1/4)x3
vmax= v = 0 ---> 108 - (3/4)x3 = 0
108 = (3/4)x2 <=> x2 = 144
x = 12
<=> t = (108/x) - (1/4)x = (108/12) - (1/4)12 = 6
Jadi, volume kubus adalah
v = x3 . t = 144 x 6 = 864 cm3
5. Pada suatu barisan aritmatik, suku kedua adalah 8, suku keempatnya adalah
14 dan suku terakhir adalah 23, maka banyaknya suku barisan tersebut adalah
.....
A. 9
B. 8
C. 7
D. 6
E. 5
Barisan aritmatik berlaku Un = a + (n-1)b
U4 = a + 3b = 14
U2 = a + b = 8
_______________
2b = 6 ----> b = 3
b = 3 ---> a + 3 = 8
--> a = 5
Un = 23 = 5 + (n-1)3
---> 18 = 3n - 3
---> 3n = 21
n = 7
6. Nilai maksimum dari x + y- 6 yang memenuhi syarat x ≥ 0, y ≥ 0, 3x +
8y ≤ 340 dan 7x +4y ≤ 280 adalah ....
A. 48
B. 49
C. 50
D. 51
E. 52
syarat
x ≥ 0
y ≥ 0
3x + 8y ≤ 340 ....... 1)
7x + 4y ≤ 280 ....... 2)
Nilai maksimum dari x + y - 6 yang memenuhi persyaratan di atas adalah
titik potong garis 1) dan 2)
7x + 4y = 280 x 2 ---> 14x + 8y = 560
3x + 8y = 340 x 1 ---> 3x + 8y = 340
________________________________
11 x = 220
x = 20
y = (280- 7 . 20)/4
= 35
Nilai maksimum dari x + y- 6 = 20 + 35 - 6 = 49
Lanjut ke nomor soal berikutnya yaa >>>>> Halaman 2
EmoticonEmoticon