Salam. Hai sahabat Ahzaa, selamat datang kembali di AhzaaNet. Hari ini kita lanjutkan lagi belajar untuk menghadapi UTBK SBMPTN khususnya dalam tes potensi akademik. Adapun sub jenis soal yang akan dibahas melalui latihan soal hari ini adalah Kemampuan Penalaran Numerik. Tes ini berisikan materi tentang Aljabar dan Aritmatika Sederhana.
 |
| source : Unsplash |
Latihan soal pada post ini merupakan kompilasi berbagai soal Kemampuan Penalaran Numerik dari soal- soal yang muncul di ujian SNMPTN maupun SBMPTN pada tahun- tahun sebelumnya. Semoga saja ada soal yang bertipe sama.
Latihan soal sudah saya lengkapi dengan kunci jawaban dan pembahasan untuk memudahkan dalam belajar.
Baik, langsung saja yaa, berikut latihan soalnya, selamat berlatih dan semoga bermanfaat.
=====================================================================================
Latihan Soal dan Pembahasan Tes Kemampuan Penalaran Numerik TPA UTBK SBMPTN 2022
=====================================================================================
1. SNMPTN/2012/TPA/811
X adalah 15% dari 3000. Apabila Y = 30% X, berapakah nilai Y?
A. 115
B. 120
C. 125
D. 130
E. 135
X = 15% * 3000
= 15/100 * 3000
= 450
Subtitusikan X ke Y,
Y = 30% * X
= 30/100 *450
= 135
2. SNMPTN/2012/TPA/811
Sepotong kayu beratnya 20 gram. Setelah dikeringkan di panas matahari,
beratnya menjadi 12 gram. Berapa persen kandungan air dalam kayu basah
tersebut?
A. 80%
B. 40 %
C.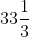 
D. 25 %
E. 20 %
Kandungan air dalam kayu yang telah menguap = berat awal- berat akhir
= 20 gram - 12 gram
= 8 gram
Presentasi kandungan air dalam kayu = perubahan berat/ berat awal * 100 %
= 8 gram/ 20 gram * 100%
= 40 %
3. SNMPTN/2012/TPA/811
Dedy dan Ambar mendaftar sebagai peserta asuransi dengan besar premi sama.
Jika untuk membayar premi gaji Dedy sebesar Rp1.500.000 dipotong 3%, dan gaji
Ambar dipotong 5%, maka gaji Ambar adalah ....
A. Rp990.000
B. Rp975.000
C. Rp950.000
D. Rp900.000
E. Rp850.000
Misal x = Gaji Dedy
y = Gaji Ambar
Premi = 3% × x
Premi = 5% × y
} 3% × x = 5% × y ⇒
y = 3%/5% * Rp 1.500.000
= Rp900.000
4. SBMPTN/2013/TPA/211
Nilai dari (2013-2015+2018-2019) + (2015-2010+2019-2018) adalah ....
A. 8
B. 6
C. 5
D. 3
E. 2
(2013-2015+2018-2019) + (2015-2010+2019-2018)
- kelompokkan terlebih dahulu bilangan- bilangan di atas menjadi seperti
berikut,
2013 -2015+2015+ 2018-2018- 2019+2019 -2010
(terdapat tiga bilangan yang saling berlawanan apabila dihitung hasilnya
adalah nol (bilangan yang berwarna merah) sehingga didapatkan 2013 - 2010 =
3
5. SBMPTN/2013/TPA/111
Jika 2013ab - 4 = 3030, maka 6039 ab = ...
A. 3034
B. 3094
C. 6039
D. 9012
E. 9102
Jika 2013ab - 4 = 3030, maka
2013ab - 4 = 3030
Maka,
2013ab = 3034
Sehingga
6039ab = 3 x 2013ab = 3 x 3034 = 9102
6. SBMPTN/2013/TPA/211
Nilai dari 0.4 + (0.8 x 0.5) + 0.7 adalah ....
A. 1.5
B. 1.44
C. 1.3
D. 0.144
E. 0.15
0.4 + (0.8 x 0.5) + 0.7
= 0.4 + (0.4) + 0.7
= 1.5
7. SNMPTN/2010/TPA/942/53
Jika x dan y bilangan bulat yang memenuhi 16 < 𝑥 < 18 dan 17 < 𝑦
< 19, maka ....
A. x < y
B. x > y
C. x = y
D. x = 2y
E. x > 2y
𝑥 dan 𝑦 adalah bilangan bulat
16 < x < 18 <=> x = 17
17 < y < 19 <=> x = 18
Jadi, x < y
8. SNMPTN/2010/TPA/942/52
Jika x adalah 12,11% dari 0,34, dan y adalah 34% dari 0,1211, maka ....
A. x = y
B. x < y
C. x > y
D. y = 100x
E. x = 100y
x = 12,11% × 0,34 =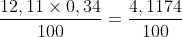 
y = 34% × 0,1211 =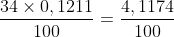 
Jadi, x = y.
9. USM STAN 2011
3,8 x 33 + 2,1 x 17 + 33 x 2,1 + 17x 3,8 =
A. 245
B. 295
C. 305
D. 345
3,8 x 33 + 2,1 x 17 + 33 x 2,1 + 17x 3,8 =
3,8 X 33 + 17 X 3,8 + 2,1 X 17 + 33 X 2,1
gunakan sifat hitung distributif
= 3,8 x(33+17) + 2,1 x (17+33)
= 3,8 x 50 + 2,1 x 50
= 50 x (3,8+2,1)
= 50 x (3,8+2,1)
= 50 x 5,9
= 295
atau
= 2,1 (17+33)+ 3,8(17+33)
= 4,9(17+33)
= 4,9(50)
= 295
10. SNMPTN/2011/TPA/796
Persegi panjang Q mempunyai panjang 2p dan lebar q. Persegi P yang
panjang sisinya p, mempunyai luas seperempat luas Q. Jadi ....
A. p = q
B. p = 2q
C. 2p = q
D. p = 4q
E. 4p = q
Luas persegi P = 1/4 * Luas persegi panjang Q
p x sisi = 1/4(2pq)
sisi = 1/2 q
Bangun persegi memiliki sisi yang sama sehingga p = 1/2 q ⇔ 2p = q.
11. USM STAN 2011
Jika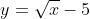 
dengan x dan y anggota bilangan asli maka ....
A. x < y
B. x > y
C. x = y
D. hubungan x dan y tidak dapat ditentukan
Hubungan x dengan adalah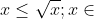 
bilangan asli. Karena =
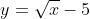maka x> y
12. SNMPTN/2011/TPA/796
Perbandingan luas sebuah lingkaran berdiameter 12 cm dengan luas
lingkaran berdiameter 4 cm adalah ....
A. 1 : 3
B. 1 : 9
C. 3 : 1
D. 4 : 1
E. 9 : 1
L1 =
L2 =
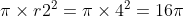
L1 ∶ L2 = 144𝜋 ∶ 16𝜋 = 9 ∶ 1
13. SNMPTN/2011/TPA/796
Diketahui dosis pemberian suatu obat sebanding dengan berat badan
pasien. Jika dosis untuk pasien dengan berat badan 45 kg adalah 12
mg obat, maka dosis yang diberkan kepada pasien dengan berat badan
30 kg adalah ....
A. 6 mg
B. 8 mg
C. 18 mg
D. 24 mg
E. 112,5 mg
Soal di atas menggunakan perbandingan senilai,
45/12 = 30/x
⇔ 45 x = 360
x = 8
14. USM STAN 2011/2012
Diketahui x dan y dua bilangan positif. Rata-rata dari 7,17 dan x
sama dengan rata-rata y dan 16. Rasio antara x dan y
berturut-turut adalah ....
A. 2:3
B. 3:2
C. 3:5
D. 5:3
Masih semangat yaa... Yuk lanjut lagi ke nomor soal berikutnya >>>> Halaman 2
No comments:
Post a Comment